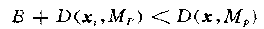K最近邻(k-Nearest Neighbor,KNN)分类算法,思路是:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
实例
有两类不同的样本数据,分别用蓝色的小正方形和红色的小三角形表示,而图正中间的那个绿色的圆所标示的数据则是待分类的数据。也就是说,现在,我们不知道中间那个绿色的数据是从属于哪一类(蓝色小正方形or红色小三角形),下面,我们就要解决这个问题:给这个绿色的圆分类。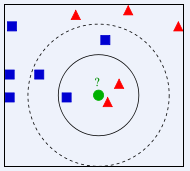
我们常说,物以类聚,人以群分,判别一个人是一个什么样品质特征的人,常常可以从他/她身边的朋友入手,所谓观其友,而识其人。我们不是要判别上图中那个绿色的圆是属于哪一类数据么,好说,从它的邻居下手。但一次性看多少个邻居呢?从上图中,你还能看到:
- 如果K=3,绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形,少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于红色的三角形一类。
- 如果K=5,绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形,还是少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于蓝色的正方形一类。
于此我们看到,当无法判定当前待分类点是从属于已知分类中的哪一类时,我们可以依据统计学的理论看它所处的位置特征,衡量它周围邻居的权重,而把它归为(或分配)到权重更大的那一类。这就是K近邻算法的核心思想。
KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
时间复杂度
KNN 算法本身简单有效,它是一种 lazy-learning 算法,分类器不需要使用训练集进行训练,训练时间复杂度为0。KNN 分类的计算复杂度和训练集中的文档数目成正比,也就是说,如果训练集中文档总数为 n,那么 KNN 的分类时间复杂度为$O(n)$。
算法要素
K 值的选择,距离度量和分类决策规则是该算法的三个基本要素:
- K 值的选择会对算法的结果产生重大影响。K值较小意味着只有与输入实例较近的训练实例才会对预测结果起作用,但容易发生过拟合;如果 K 值较大,优点是可以减少学习的估计误差,但缺点是学习的近似误差增大,这时与输入实例较远的训练实例也会对预测起作用,使预测发生错误。在实际应用中,K 值一般选择一个较小的数值,通常采用交叉验证的方法来选择最优的 K 值。随着训练实例数目趋向于无穷和 K=1 时,误差率不会超过贝叶斯误差率的2倍,如果K也趋向于无穷,则误差率趋向于贝叶斯误差率。
- 该算法中的分类决策规则往往是多数表决,即由输入实例的 K 个最临近的训练实例中的多数类决定输入实例的类别
- 距离度量一般采用 Lp 距离,当p=2时,即为欧氏距离,在度量之前,应该将每个属性的值规范化,这样有助于防止具有较大初始值域的属性比具有较小初始值域的属性的权重过大。
算法实现
算法步骤:
(1)计算已知类别数据集中的点与当前点之间的距离
(2)按照距离递增次序排序
(3)选取与当前点距离最小的K个点
(4)确定前K个点所在类别出现的频率
(5)返回前K个点出现频率最高的类别作为当前点的预测分类
python3实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19#k-近邻算法
#计算距离
def classify0(inX,dataSet,labels,k):
dataSetSize=dataSet.shape[0] #shape读取数据矩阵第一维度的长度
diffMat = tile(inX, (dataSetSize, 1)) - dataSet #tile重复数组inX,有dataSet行 1个dataSet列,减法计算差值
sqDiffMat=diffMat**2 #**是幂运算的意思,这里用的欧式距离
sqDisttances=sqDiffMat.sum(axis=1) #普通sum默认参数为axis=0为普通相加,axis=1为一行的行向量相加
distances=sqDisttances**0.5
sortedDistIndicies=distances.argsort() #argsort返回数值从小到大的索引值(数组索引0,1,2,3)
#选择距离最小的k个点
classCount={}
for i in range(k):
voteIlabel=labels[sortedDistIndicies[i]] #根据排序结果的索引值返回靠近的前k个标签
classCount[voteIlabel]=classCount.get(voteIlabel,0)+1 #各个标签出现频率
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) #排序频率
#!!!!! classCount.iteritems()修改为classCount.items()
#sorted(iterable, cmp=None, key=None, reverse=False) --> new sorted list。
# reverse默认升序 key关键字排序itemgetter(1)按照第一维度排序(0,1,2,3)
return sortedClassCount[0][0] #找出频率最高的
算法优缺点
优点:
精度高、对异常值不敏感、无数据输入假定。
KNN算法不仅可以用于分类,还可以用于回归。通过找出一个样本的k个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。
缺点:
当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。 该算法只计算“最近的”邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。无论怎样,数量并不能影响运行结果。可以采用权值的方法(和该样本距离小的邻居权值大)来改进。
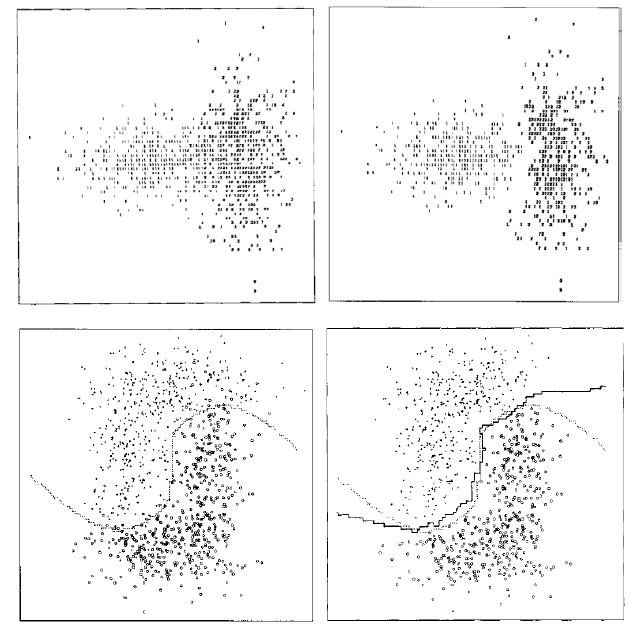
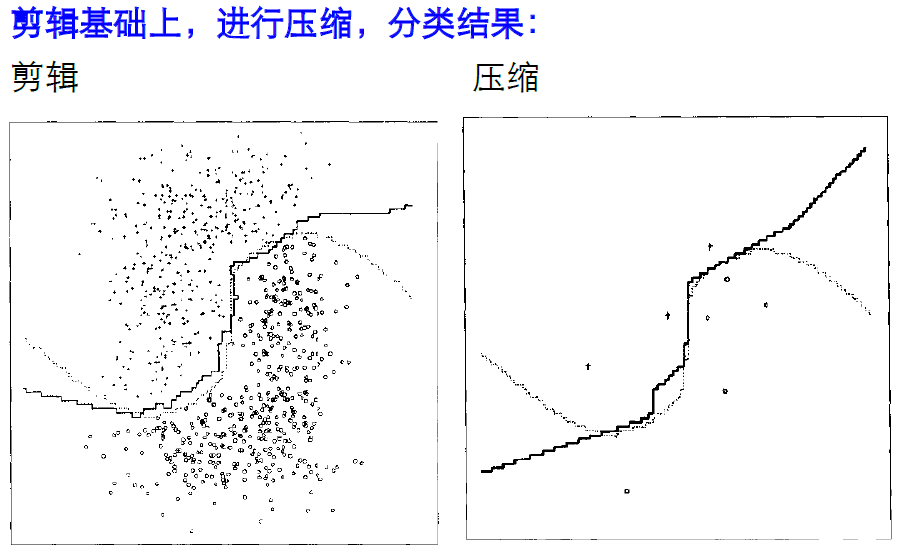
该方法的另一个不足之处是计算量较大,因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。目前常用的解决方法是事先对已知样本点进行剪辑,事先去除对分类作用不大的样本。该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
适用数据范围:
数值型和标称型。
标称型:一般在有限的数据中取,而且只存在‘是’和‘否’两种不同的结果(一般用于分类)
数值型:可以在无限的数据中取,而且数值比较具体化,例如4.02,6.23这种值(一般用于回归分析)
算法改进
摘自《模式识别》。
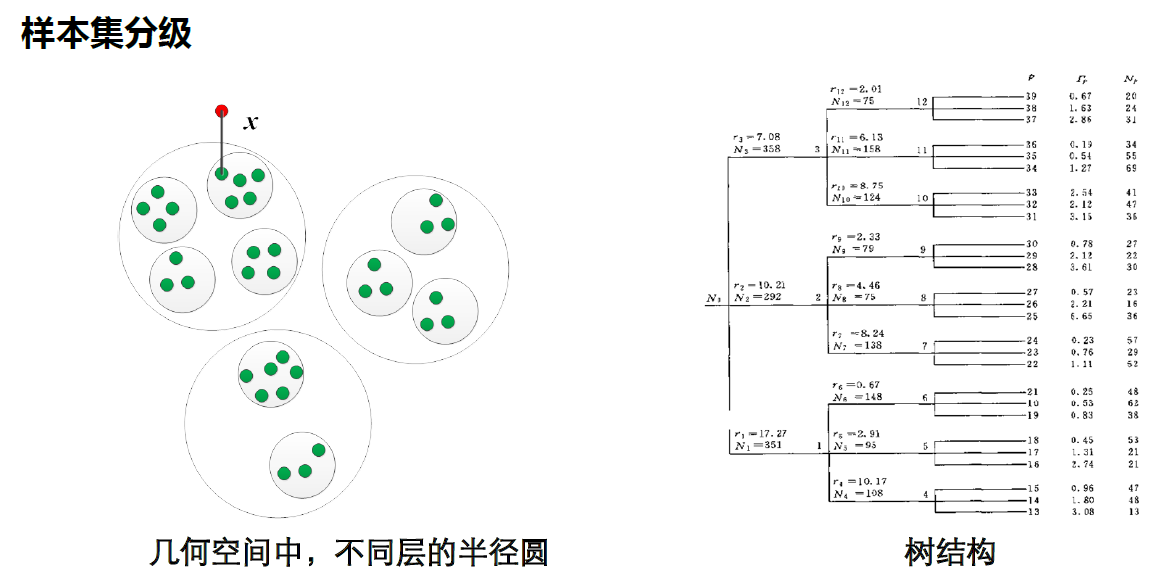
快速搜索近邻法
近邻法当样本数目较多时才会取得好的性能,但是新样本需要与每一个样本计算距离,然后再通过排序找到最近邻或前K个最近邻。当样本数目较多时计算量会非常大。
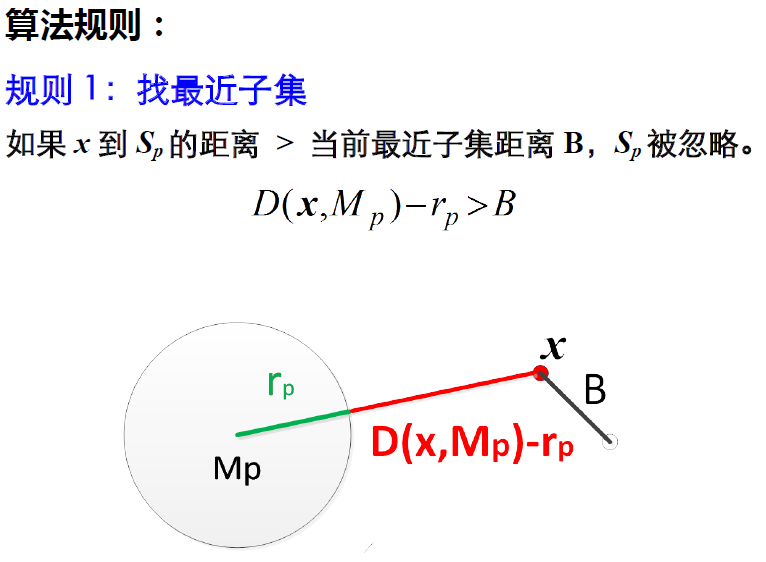
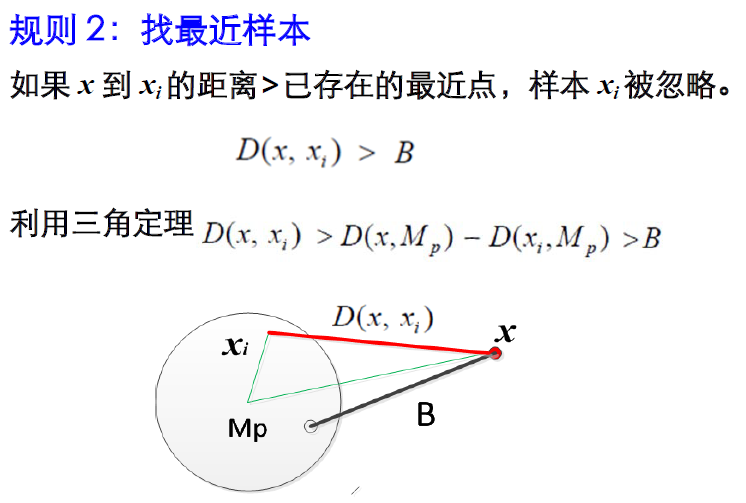
为此,人们采用分支界定算法的思想设计了快速算法。基本思想是:
将样本分成不相交的子集,基于子集的搜索。