AdaBoost

1. AdaBoost算法

Boosting是一种常用的统计学习方法，应用广泛且有效，在分类问题中，它通过改变训练样本的权重，学习多个分类器，并将这些分类器进行线性组合，提高分类的性能。

AdaBoost算法是Boosting中的代表算法。对于提升方法来说，有两个问题需要解决：

在每一轮中如何改变训练数据的权值或概率分布；
如何将弱分类器组合成一个强分类器。

AdaBoost的做法为：

对于第一个问题，AdaBoost提高那些被前一轮弱分类器错误分类样本的权值，而降低那些被正确分类样本的权值；
对于第二个问题，AdaBoost采用加权多数表决的方式。

AdaBoost的主要优点：

AdaBoost作为分类器时，分类精度很高；
在AdaBoost的框架下，可以使用各种回归分类模型来构建弱学习器，十分灵活；
作为简单的二分类器时，构造简单，结果可理解；
不容易发生过拟合。

AdaBoost的主要缺点：

对异常样本敏感，异常样本在迭代中可能会获得较高的权重，影响最终的强学习器的预测准确性。

现在叙述AdaBoost算法，假设给定一个二类分类的训练数据集

$T = \{(\pmb{x}_1,y_1), (\pmb{x}_2,y_2), \cdots, (\pmb{x}_N,y_N)\}$

其中，每个样例点由实例和标记组成，实例$\pmb{x}_i \in \mathbf{R}^n$，标记$y_i \in {-1,+1}$，AdaBoost算法如下：
此处输入图片的描述

对AdaBoost算法作如下说明：
步骤（1）假设训练数据集具有均匀的权值分布，即每个训练样本在基分类器的学习中作用相同，这一假设保证第1步能够在原始数据上学习基本分类器$G_1(\pmb{x})$。
步骤（2）AdaBoost反复学习基本分类器，在每一轮$m=1,2,\cdots,M$顺次地执行下列操作：
（i）使用当前分布$D_m$加权的训练数据集，学习基本分类器$D_m(\pmb{x})$；
（ii）计算基本分类器$G_m (\pmb{x})$在加权训练数据集上的分类错误率：

$e_m = \sum_{i=1}^N P(G_m(\pmb{x}_i) \neq y_i) = \sum_{G_m(\pmb{x}_i) \neq y_i} w_{mi} \tag{8.8}$

$w{mi}$表示第$m$轮中第$i$个实例的权值，$\sum{i=1}^N w_{mi} = 1$。这表明，$G_m(\pmb{x})$在加权的训练数据集上的分类误差率是被$G_m(\pmb{x})$误分类样本的权值和。
（iii）计算基本分类器$G_m(\pmb{x})$的系数$\alpha_m$。$\alpha_m$表示$G_m(\pmb{x})$在最终分类器中的重要性。由式（8.2）可知，当$e_m \leq \frac{1}{2}$时，$\alpha_m \geq 0$，并且$\alpha_m$随着$e_m$的减小而增大，所以分类误差率越小的基本分类器在最终分类器中的作用越大。
（iiii）更新训练数据的权值分布为下一轮做准备。式（8.4）可以写成：

$w_{m+1,i} = \begin{cases} \frac{w_{mi}}{Z_m} e^{- \alpha_m}, \quad G_m(\pmb{x}_i) = y_i \\ \frac{w_{mi}}{Z_m} e^{\alpha_m}, \quad G_m(\pmb{x}_i) \neq y_i \end{cases}$

由此可知，被基本分类器$G_m(\pmb{x})$误分类样本的权值得以扩大，而被正确分类样本的权值却得以缩小。两者相比较，误分类样本的权值被放大$e^{2 \alpha_m} = \frac{1 - e_m}{e_m}$倍。因此，误分类样本在下一轮学习中起更大的作用。不改变所给的训练数据，而不断改变训练数据权值的分布，使得训练数据在基本分类器的学习中其不同的作用，这是AdaBoost的一个特点。

步骤（3）线性组合$f(\pmb{x})$实现$M$个基本分类器的加权表决。系数$\alpha_m$表示了基本分类器$G_m(\pmb{x})$的重要性。这里，所有$\alpha_m$之和并不为1，$f(\pmb{x})$的符号决定了实例$\pmb{x}$的类，$f(\pmb{x})$的绝对值表示分类的确信度，利用基本分类器的线性组合构建最终分类器是AdaBoost的另一特点。

2. AdaBoost算法的训练误差分析

AdaBoost最基本的性质是它能在学习过程中不断减少训练误差，即在训练数据集上的分类误差率。
定理1：AdaBoost算法最终分类器的训练误差界为

$\frac{1}{N} \sum_{i=1}^N I(G_m(\pmb{x}_i) \neq y_i) \leq \frac{1}{N} \sum_{i=1} \exp(- y_i f(\pmb{x}_i))= \prod_{m} Z_m$

证明：当$G_m(\pmb{x}_i) \neq y_i$时，$y_i f(\pmb{x}_i) < 0$，因而$\exp(- y_i f(\pmb{x}_i)) \geq 1$，由此可直接推导出前半部分。
后半部分的推导需要用到$Z_m$的定义式（8.5）及式（8.4）的变形：

$w_{mi} \exp(- \alpha_m y_i G_m (\pmb{x}_i)) = Z_m w_{m+1,i}$

现推导如下：

$\begin{align} \frac{1}{N} \sum_i \exp(-y_i f(\pmb{x}_i)) &= \frac{1}{N} \sum_i \exp(- \sum_{m=1}^M \alpha_m y_i G_m(\pmb{x}_i)) \nonumber \\ &= \sum_i w_{1i} \prod_{m=1}^M \exp (- \alpha_m y_i G_m(\pmb{x}_i)) \nonumber \\ &= Z_1 \sum_i w_{2i} \prod_{m=2}^M \exp(- \alpha_m y_i G_m(\pmb{x}_i)) \nonumber \\ &= Z_1 Z_2 \sum_i w_{3i} \prod_{m=3}^M \exp(- \alpha_m y_i G_m(\pmb{x}_i)) \nonumber \\ &= \cdots \nonumber \\ &= Z_1 Z_2 \cdots Z_{M-1} \sum_i w_{Mi} \exp(- \alpha_M y_i G_M(\pmb{x}_i)) \nonumber \\ &= \prod_{m=1}^M Z_m \nonumber \end{align}$

这一定理说明，可以在每一轮中选取适当的$G_m$使得$Z_m$最小，从而使训练误差下降最快。

定理2：二类分类问题AdaBoost的训练误差界

$\prod_{m=1}^M Z_m = \prod_{m=1}^M [2 \sqrt{e_m(1-e_m)}] = \prod_{m=1}^M \sqrt{(1-4 \gamma_m^2)} \leq \exp(-2 \sum_{m=1}^M \gamma_m^2)$

式中$\gamma_m = \frac{1}{2} - e_m$。
证明：由$Z_m$的定义式（8.5）及式（8.8）得

$\begin{align} Z_m &= \sum_{i=1}^N w_{mi} \exp(- \alpha_m y_i G_m(\pmb{x}_i)) \nonumber \\ &= \sum_{y_i = G_m(\pmb{x}_i)} w_{mi} e^{- \alpha_m} + \sum_{y_i \neq G_m(\pmb{x}_i)} w_{mi} e^{\alpha_m} \nonumber \\ &= (1-e_m) e^{-\alpha_m} + e_m e^{\alpha_m} \nonumber \\ &= 2 \sqrt{e_m (1 - e_m)} \nonumber \\ &= \sqrt{1 - 4 \gamma_m^2} \nonumber \end{align}$

其中对于$\alpha_m$的化简需要将$\alpha_m = \frac{1}{2} \log \frac{1 - e_m}{e_m}$带入。
至于不等式

$\prod_{m=1}^M \sqrt{(1-4 \gamma_m^2)} \leq \exp(-2 \sum_{m=1}^M \gamma_m^2)$

则可先由$e^x$和$\sqrt{1-x}$在点$x=0$的泰勒展开式推出不等式$\sqrt{(1-4 \gamma_m^2)} \leq \exp(-2 \gamma_m^2)$，进而得到。

推论：如果存在$\gamma > 0$，对所有$m$有$\gamma_m \geq \gamma$，则

$\frac{1}{N} \sum_{i=1}^N I(G_m(\pmb{x}_i) \neq y_i) \leq \exp(-2M \gamma^2)$

这表明在此条件下AdaBoost的训练误差是以指数速率下降的。
注意，AdaBoost算法不需要知道下界$\gamma$，与早期的提升方法不同，AdaBoost具有适应性，即它梦适应弱分类器各自的训练误差率。

3. AdaBoost算法的解释

AdaBoost算法还有一个解释，即可认为AdaBoost算法是模型为加法模型、损失函数为指数函数、学习算法为前向分步算法时的二类学习算法。

3.1. 前向分步算法

考虑加法模型（additive model）

$f(\pmb{x}) = \sum_{i=1}^M \beta_m b(\pmb{x};\gamma_m)$

其中，$b(\pmb{x};\gamma_m)$为基函数，$\gamma_m$为基函数的参数，$\beta_m$为基函数的系数。
在给定训练数据及损失函数$L(y,f(\pmb{x}))$的条件下，学习算法模型$f(\pmb{x})$称为经验风险最小化即损失函数极小化问题：

$\min_{\beta_m,\gamma_m} \sum_{i=1}^N L(y_i, \sum_{m=1}^M \beta_m b(\pmb{x}_i;\gamma_m))$

通常这是一个复杂的优化问题。前向分步算法（forward stagewise algorithm）求解这一优化问题的想法：因为学习的是加法模型，如果能够从前向后，每一步只学习一个基函数及其系数，逐步逼近优化目标函数式，那么就可以简化优化的复杂度。
具体地，每步只需要优化如下损失函数：

$\min_{\beta,\gamma} \sum_{i=1}^N L(y_i,\beta b(\pmb{x}_i;\gamma))$

给定训练数据集$T={(\pmb{x}_1,y_1),(\pmb{x}_2,y_2),\cdots, (\pmb{x}_N,y_N)}$，$\pmb{x} \in \mathbf{R}^n$，$y_i \in {-1,+1}$，损失函数$L(y,f(\pmb{x}))$和基函数的集合${b(\pmb{x};\gamma)}$，学习加法模型$f(\pmb{x})$的前向分步算法如下：
此处输入图片的描述

这样，前向分步算法将同时求解从$m=1$到$M$所有的参数$\beta_m,\gamma_m$的优化问题简化为逐次求解各个$\beta_m,\gamma_m$的优化问题。

3.2. 前向分步算法与AdaBoost

定理：AdaBoost算法是前向分步加法算法的特例。模型是由基本分类器组成的加法模型，损失函数是指数函数。
证明：前向分步算法学习的是加法模型，当基函数为基本分类器时，该加法模型等价于AdaBoost的最终分类器

$f(\pmb{x}) = \sum_{i=1}^M \alpha_m G_m(\pmb{x})$

由基本分类器$G_m(\pmb{x})$及其系数$\alpha_m$组成，$m=1,2,\cdots,M$。前向分步算法逐一学习基函数，这一过程与AdaBoost算法注意学习基本分类器的过程一致。
下面证明前向分步算法的损失函数是指数损失函数

$L(y,f(\pmb{x})) = \exp[-yf(\pmb{x})]$

时，其学习的具体操作等价于AdaBoost算法学习的具体操作。
假设经过$m-1$轮迭代前向分步算法已经得到$f_{m-1} (\pmb{x})$：

$\begin{align} f_{m-1}(\pmb{x}) &= f_{m-2}(\pmb{x}) + \alpha_{m-1} G_{m-1} (\pmb{x}) \nonumber \\ &=\alpha_1 G_1 (\pmb{x})+ \cdots + \alpha_{m-1} G_{m-1} (\pmb{x}) \nonumber \end{align}$

在第$m$轮迭代得到$\alpha_m,G_m(\pmb{x})$和$f_m(\pmb{x})$。

$f_m(\pmb{x}) = f_{m-1}(\pmb{x}) + \alpha_m G_m(\pmb{x})$

目标是使前向分步算法得到的$\alpha_m$和$G_m(\pmb{x})$使$f(\pmb{x})$在训练数据集$T$上的指数损失最小，即

$(\alpha_m,G_m(\pmb{x})) = \arg \min_{\alpha,G} \sum_{i=1}^N \exp[-y_i(f_{m-1}(\pmb{x}_i) + \alpha G(\pmb{x}_i))]$

上式还可以表示成

$(\alpha_m,G_m(\pmb{x})) = \arg \min_{\alpha,G} \sum_{i=1}^N \bar{w}_{mi} \exp[- y_i \alpha G(\pmb{x}_i)]$

其中，$\bar{w}{mi} = \exp[-y_i f{m-1}(\pmb{x}i)]$，因为$\bar{w}{mi}$既不依赖$\alpha$也不依赖于$G$,所以与最小化无关。但$\bar{w}{mi}$依赖于$f{m-1}(\pmb{x})$，随着每一轮迭代而发生改变。
现在需要证明上式达到最小的$\alpha_m^$和$G_m^(\pmb{x})$就是AdaBoost算法所得到的$\alpha_m$和$G_m(\pmb{x})$，求解上式可分为两步：

（1）求解$G_m^* (\pmb{x})$。
对任意$\alpha > 0$,使式中最小的$G(\pmb{x})$由下式得到：

$G_m^* (\pmb{x}) = \arg \min_G \sum_{i=1}^N \bar{w}_{mi} I(y_i \neq G(\pmb{x}_i))$

其中，$\bar{w}{mi} = \exp[-y_i f{m-1}(\pmb{x}_i)]$。
此分类器$G_m^*(\pmb{x})$即为AdaBoost算法的基本分类器$G_m(\pmb{x})$，因为它是使第$m$轮加权训练数据分类误差率最小的基本分类器。

（2）求解$\alpha_m^*$。

$\begin{align} h(\alpha) &=\sum_{i=1}^N \bar{w}_{mi} \exp[-y_i \alpha G(\pmb{x}_i)] \nonumber \\ &= \sum_{y_i = G_m(\pmb{x}_i)} \bar{w}_{mi} e^{- \alpha} + \sum_{y_i \neq G_m(\pmb{x}_i)} \bar{w}_{mi} e^{\alpha} \nonumber \\ &= (e^{\alpha} - e^{- \alpha}) \sum_{i=1}^N \bar{w}_{mi} I(y_i \neq G(\pmb{x}_i)) + e^{- \alpha} \sum_{i=1}^N \bar{w}_{mi} \nonumber \end{align}$

将以求得的$G_m^*(\pmb{x})$带入上式，对$\alpha$求导并使导数为0，即求得使原式最小的$\alpha$。
令$e_m$表示分类错误率：

$e_m = \frac{\sum_{i=1}^N \bar{w}_{mi} I(y_i \neq G_m(\pmb{x}_i))}{\sum_{i=1}^N \bar{w}_{mi}} = \sum_{i=1}^N w_{mi} I(y_i \neq G_m(\pmb{x}_i))$

则有

$\begin{equation} \frac{\partial h(\alpha)}{\partial \alpha} = (e^{\alpha} + e^{- \alpha}) \sum_{i=1}^N \bar{w}_{mi} I(y_i \neq G_m(\pmb{x}_i)) - e^{- \alpha} \sum_{i=1}^N \bar{w}_{mi} = 0 \nonumber \\ (e^{\alpha} + e^{- \alpha}) \frac{\sum_{i=1}^N \bar{w}_{mi} I(y_i \neq G_m(\pmb{x}_i))}{\sum_{i=1}^N \bar{w}_{mi}} - e^{- \alpha} = 0 \nonumber \\ (e^{\alpha} + e^{- \alpha}) e_m - e^{- \alpha} = 0 \nonumber \end{equation}$

求得

$\alpha_m^* = \frac{1}{2} \log \frac{1-e_m}{e_m}$

这里的$\alpha_m^*$与AdaBoost算法在第2（c）步求得的$\alpha_m$完全一致。
最后再看每一轮样本权值的更新，由

$f_m(\pmb{x}) = f_{m-1}(\pmb{x}) + \alpha_m G_m(\pmb{x})$

以及$\bar{w}{mi} = \exp[-y_i f{m-1}(\pmb{x}_i)]$，可得

$\bar{w}_{m+1,i} = \bar{w}_{m,i} \exp[-y_i \alpha_m G_m(\pmb{x})]$

这里与AdaBoost算法第2（d）步的样本权值更新只相差规范化因子，因而等价。

4. AdaBoost多分类和回归

4.1. 多分类

原始的AdaBoost算法是针对二分类问题的，多分类问题采用的也是将其分解为多个二分类问题。而SAMME和SAMME.R算法不采用这种思路，只是二分类的推广，也是加法模型，指数损失函数和前向分步算法，而且每个弱分类器的正确率只要大于0.5即可。
假设训练集$T = {(\pmb{x}1,y_1),(\pmb{x}_2,y_2),\cdots,(\pmb{x}_n,y_n)}$，训练集在第$k$个弱分类器上的样本权重是$(w{k1},w{k2},\cdots,w{kn}),w_{1i} = \frac{1}{n},i=1,2,\cdots,n$，输出$y_i \in {1,2,\cdots,K}$，$K$是类别个数。

SAMME

此处输入图片的描述
SAMME.R

参考文献：Zhu J, Zou H, Rosset S, et al. Multi-class AdaBoost[J]. Statistics & Its Interface, 2006, 2(3):349-360.

4.2. 回归

假设训练集为$T={(\pmb{x}_1,y_1),(\pmb{x}_2,y_2),\cdots,(\pmb{x}_N,y_N)}$。
输入：训练数据集，弱学习算法和弱学习器个数T
输出：最终的强学习器$G(\pmb{x})$

初始化样本权重$D1 = (w{11},w{12},\cdots,w{1n}),\quad w_{1i}=\frac{1}{n},\quad i=1,2,\cdots,N$。
对$m=1,2,\cdots,T$：
1. 使用具有样本权重$Dm$的训练数据和弱学习器算法得到弱学习器$G_m(\pmb{x})$;
2. 计算弱学习器在训练集上上的误差$e{mi} = L(|y_i - G_m(\pmb{x}_i)|)$，损失函数$L$可以具有任意形式但必须保证$L \in [0,1]$，令$E_m = sup|y_i - G_m(\pmb{x}_i)|,i=1,2,\cdots,N$，即训练集上的最大误差，然后我们会有三种可选用的损失函数：
```
 &emsp;&emsp;&emsp;&emsp;1. 线性误差：$e_{mi} = \frac{|y_i - G_m(\pmb{x}_i)|}{E_m}$；  
 &emsp;&emsp;&emsp;&emsp;2. 平方误差：$e_{mi} = \frac{|y_i - G_m(\pmb{x}_i)|^2}{E_m}$；  
 &emsp;&emsp;&emsp;&emsp;3. 指数误差：$e_{mi} = 1 - \exp[\frac{|y_i - G_m(\pmb{x}_i)|}{E_m}]$；  
```
3. 利用每个样本的相对误差，计算回归误差率$em = \sum{i=1}^N w{mi} e{mi}$；
4. 计算弱学习器的权重系数$\alpham = \frac{e_m}{1 - e_m}$；
5. 更新样本权重$w{m+1,i} = \frac{w{mi}}{Z_m} e_m^{1 - e{mi}}$，其中$Zm$为归一化因子，$Z_m = \sum{i=1}^N w{mi} e_m^{1 - e{mi}}$；
根据$T$个弱学习器得到最终的强学习器，利用强学习器进行预测的策略为： $G = inf\{y \in Y: \sum_{m:G_m \leq y} \log(\frac{1}{e_m}) \geq \frac{1}{2} \sum_m \log(\frac{1}{e_m}) \}$ 计算的是加权中值，对于实例$\pmb{x}_i$，每一个弱学习器$G_m$都会产生输出概率$y_i^{(m)}$，并且弱学习器$G_m$对应的权重系数为$\alpha_m$，我们对所有弱学习器的输出值进行排序并重新标记： $y_i^{(1)} < y_i^{(2)} < \cdots < y_i^{(T)}$ 但保持每个学习器$G_m$与其对应的权重系数$\alpha_m$不变。按照上述排序依次累加各弱学习器对应的$\log(\frac{1}{e_m})$直到找到满足公式中不等式的最小的$m$值，则将弱学习器$G_m$的预测值作为最终强学习器的预测值。

参考文献：Drucker H. Improving Regressors using Boosting Techniques[C]// Fourteenth International Conference on Machine Learning. Morgan Kaufmann Publishers Inc. 1997:107-115.

5. sklearn使用

sklearn中AdaBoost类库包含AdaBoostClassifier和AdaBoostRegressor两个，其中AdaBoostClassifier用于分类，AdaBoostRegressor用于回归。

AdaBoostClassifier：

1	class sklearn.ensemble.AdaboostClassifier(base_estimator=None, n_estimators=50, learning_rate=1.0, algorithm='SAMME.R', random_state=None)

AdaBoostRegressor:

1	class sklearn.ensemble.AdaBoostRegressor(base_estimator=None, n_estimators=50, learning_rate=1.0, loss=’linear’, random_state=None)

框架参数
此处输入图片的描述
algorithm：AdaBoostClassifier中有一个algorithm参数，而在AdaBoostRegressor中没有。这是因为sklearn中实现了两种AdaBoost分类算法，SAMME和SAMME.R。两者的主要区别是弱学习器权重的度量，SAMME使用的是上文介绍过的二分类AdaBoost算法的扩展，即用对样本集分类效果作为弱学习器的权重。而SAMME.R使用了概率度量的连续值，迭代一般比SAMME快，因此AdaBoostClassifier的默认算法algorithm的值为SAMME.R。如果使用SAMME.R，则弱分类学习器base_estimator必须限制使用支持概率预测的分类器，而SAMME算法则没有这个限制。

函数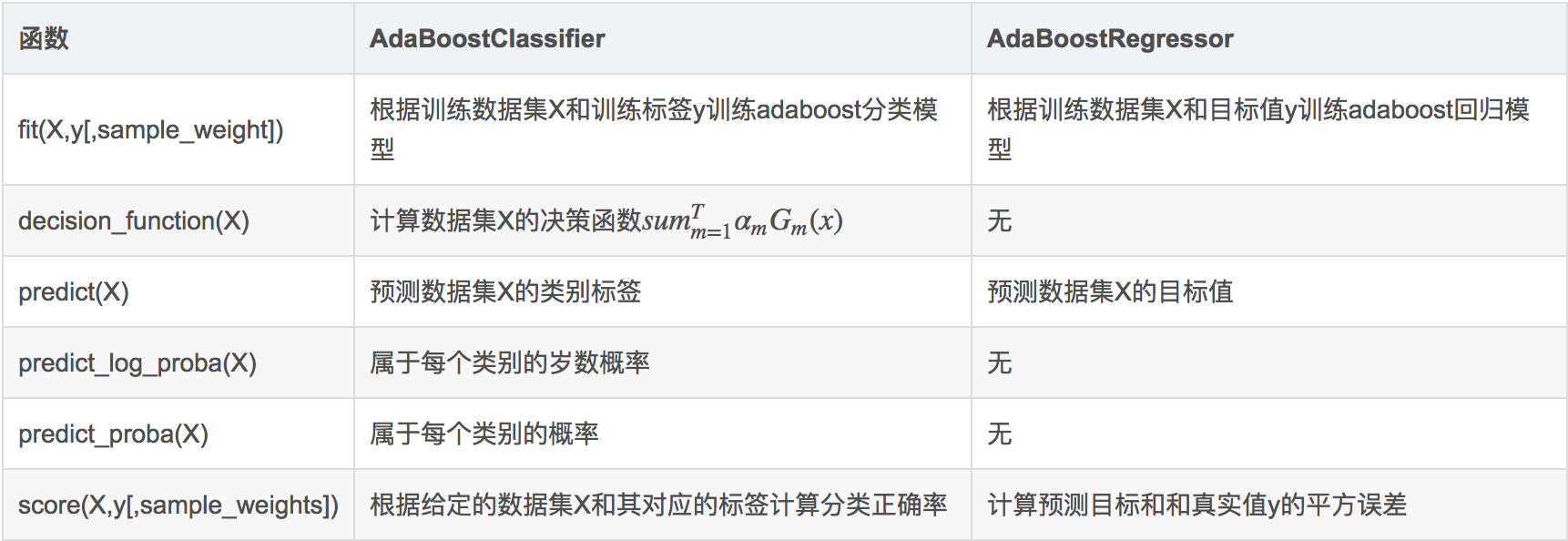
此处输入图片的描述
属性